Building the Self-Attention Mechanism from scratch

In this project, I build the basic self-attention mechanism (used in large language models) to calculate the attention scores of an input sentence.

Published

12 January 2025

In this project, we’re going to implement the Self-Attention mechanism used in the Transformer architecture.

This post will begin with a short recap of how the attention mechanism works, followed by a code-along section where we implement the attention mechanism for calculating the attention scores of input text sentences.

Here’s the structure for this project post:

1. Quick recap on how Self-Attention works
2. Code Implementation of Self-Attention Mechanism
3. References

*Additionally, I’d like to mention that I did a detailed technical writeup on how the Self-Attention mechanism works geometrically. Please check it out first to get a good geometric intuition for the roles of the K,Q,V matrices.

$~ \\$

1. Quick Recap on how Self-Attention works

The (scaled dot-product) Self-Attention mechanism is defined mathematically as:

$\boxed{\text{Attention}(K,Q,V) = \text{softmax}(\frac{QK^T}{\sqrt{d_k}})V}$

Visually, the operations that happen within the scaled dot-product self-attention formula are like so:

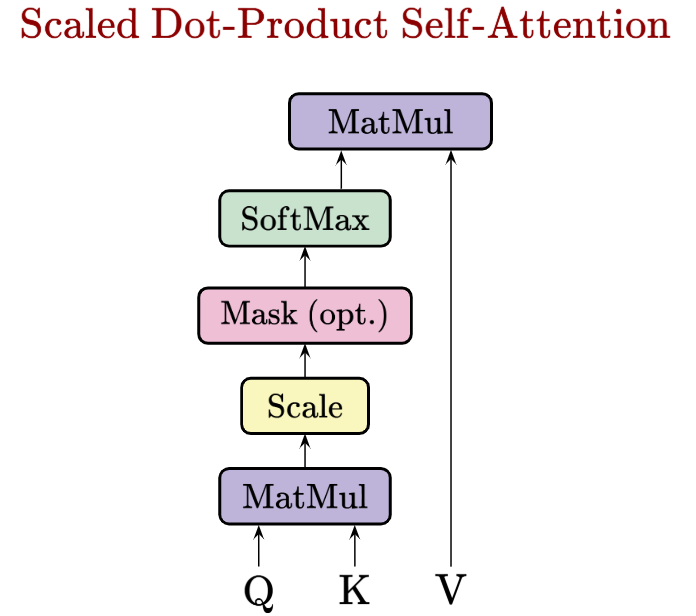
We learned in the other technical writeup that the Keys and Queries matrices help us find the ideal embedding space to find pairwise similarities between our embedding vectors. The resulting computation allows us to find the attention scores of each token - so the Keys and Queries matrices tell us how much focus each token should get.

Then, we’ll use the Attention Weights obtained from the Keys and Queries matrices to optimize the embedding in our Values matrix embedding space, which gives us context-aware, optimized embeddings of our tokens.

Here’s a visualization of how the context-aware, optimized token embeddings might be obtained after passing our original token embeddings into the Self-Attention mechanism.

Downstream, this attention output (the contextualized token embeddings) might be passed into a neural network for further refining, then each final token embedding might be mapped into a probability distribution over the entire vocabulary. This allows us to do next-word prediction, and create useful sentences like GPT does.

Alright, now we’re ready to implement the attention mechanism in code.

$~ \\$

2. Code Implementation of Self-Attention Mechanism

This code implementation will reflect my attempt to modify Sebastian Raschka’s implementation.

Embedding an Input Sentence

Let’s begin with an input sentence “Life is short, eat dessert first”. We need to create a sentence embedding before passing this input through the self-attention mechanism.

For the sake of simplicity, we’ll only consider words in the input sentence, but in practice, most implementations would have a training dataset with many thousands of words.

To embed the words in our input sentence, we’ll run through the following procedure:

Create a word-to-index dictionary of our input sentence after sorting the words alphabetically
Map the words in the original unsorted sentence to their corresponding indices. Store the indexed unsorted input sentence as a PyTorch tensor for further numerical processing
Map each word to a 16-dimensional vector via a PyTorch embedding layer

Let’s go through each one, step-by-step.

$~ \\$

Step 1: Create a word-to-index dictionary of our input sentence after sorting the words alphabetically

Input:

sentence = "Life is short, eat dessert first"

dc = {s:i for i,s in enumerate(sorted(sentence.replace(',','').split()))}
print(dc)

Output:

{'Life': 0, 'dessert': 1, 'eat': 2, 'first': 3, 'is': 4, 'short': 5}

$~ \\$

Step 2: Map the words in the original unsorted sentence to their corresponding indices, then store the indexed unsorted input sentence as a PyTorch tensor for further numerical processing

Input:

import torch

sentence_int = torch.tensor( [ dc[s] for s in sentence.replace(',','').split()])
print(sentence_int)

Output:

tensor([0, 4, 5, 2, 1, 3])

$~ \\$

Step 3: Map each word to a 16-dimensional vector via a PyTorch embedding layer

Input:

torch.manual_seed(42)
embed = torch.nn.Embedding(6,16)
embedded_sentence = embed(sentence_int).detach()

print(embedded_sentence)
print(embedded_sentence.shape)

Output:

tensor([[ 1.9269,  1.4873,  0.9007, -2.1055,  0.6784, -1.2345, -0.0431, -1.6047,
         -0.7521,  1.6487, -0.3925, -1.4036, -0.7279, -0.5594, -0.7688,  0.7624],
        [ 1.4451,  0.8564,  2.2181,  0.5232,  0.3466, -0.1973, -1.0546,  1.2780,
         -0.1722,  0.5238,  0.0566,  0.4263,  0.5750, -0.6417, -2.2064, -0.7508],
        [ 0.0109, -0.3387, -1.3407, -0.5854,  0.5362,  0.5246,  1.1412,  0.0516,
          0.7440, -0.4816, -1.0495,  0.6039, -1.7223, -0.8278,  1.3347,  0.4835],
        [-1.3847, -0.8712, -0.2234,  1.7174,  0.3189, -0.4245,  0.3057, -0.7746,
         -1.5576,  0.9956, -0.8798, -0.6011, -1.2742,  2.1228, -1.2347, -0.4879],
        [ 1.6423, -0.1596, -0.4974,  0.4396, -0.7581,  1.0783,  0.8008,  1.6806,
          1.2791,  1.2964,  0.6105,  1.3347, -0.2316,  0.0418, -0.2516,  0.8599],
        [-0.9138, -0.6581,  0.0780,  0.5258, -0.4880,  1.1914, -0.8140, -0.7360,
         -1.4032,  0.0360, -0.0635,  0.6756, -0.0978,  1.8446, -1.1845,  1.3835]])
torch.Size([6, 16])

$~ \\$

Defining the Weight Matrices

Recall that for a given input $X$, we pass it through the weight matrices $W_Q, W_K, W_V$ to obtain the Queries, Keys and Values matrices respectively.

The scaled dot-product self-attention mechanism utilizes these three weight matrices and optimizes them as model parameters during training.

Since we are computing the dot product between the Queries and Keys matrices later, we need each row in the two weight matrices to have the same number of elements. On the other hand, the number of elements in each row of the Values matrix is arbitrary.

So, we’ll set $d_q = d_k = 24$ and $d_q$ = 28 arbitrarily, such that:

$W_K$ has dimensions $d \times d_K = 16 \times 24$
$W_Q$ has dimensions $d \times d_Q = 16 \times 24$
$W_V$ has dimensions $d \times d_V = 16 \times 28$

(Given our X is of dimensions 6x16.)

We’ll define the weight matrices like so:

Input:

torch.manual_seed(42)
d = embedded_sentence.shape[1]

d_k, d_q, d_v = 24, 24, 28

W_K = torch.nn.Parameter(torch.rand(d,d_k))
W_Q = torch.nn.Parameter(torch.rand(d,d_q))
W_V = torch.nn.Parameter(torch.rand(d,d_v))

$~ \\$

Computing the Attention Weights from K,Q

Now, we’ll compute the unnormalized attention weights (also called attention scores) for the Keys, Queries and Values matrices.

We need to first compute the Q,K,V matrices via matrix multiplication between the weight matrices and the embedded vectors:

$K = XW_K$
$Q = XW_Q$
$V = XW_V$

Input:

K = embedded_sentence @ W_K
Q = embedded_sentence @ W_Q
V = embedded_sentence @ W_V

print(K.shape)
print(Q.shape)
print(V.shape)

Output:

torch.Size([6, 24])
torch.Size([6, 24])
torch.Size([6, 28])

$~ \\$

Then, we will proceed to find the attention scores from the dot product of K and Q, followed by SoftMax scaling to obtain the attention weights.

Input:

import math
import torch.nn.functional as F

attention_scores = K @ Q.T
attention_scores = attention_scores / math.sqrt(d_k)
attention_weights = F.softmax(attention_scores, dim= -1) # dim = -1 ensures softmax is applied along each row

print(attention_weights)

Output:

tensor([[1.4928e-02, 2.5604e-05, 5.2063e-04, 9.8024e-01, 5.9773e-10, 4.2890e-03],
        [4.9262e-20, 5.3068e-10, 1.7273e-17, 2.0560e-22, 1.0000e+00, 1.1476e-16],
        [4.8625e-02, 1.8945e-04, 4.8195e-03, 9.3794e-01, 3.6255e-06, 8.4234e-03],
        [1.1822e-02, 8.9849e-16, 5.7813e-07, 9.8818e-01, 3.4392e-29, 2.2000e-07],
        [0.0000e+00, 6.7095e-29, 5.6052e-45, 0.0000e+00, 1.0000e+00, 1.4013e-44],
        [8.2369e-01, 1.8583e-04, 3.6337e-02, 1.2967e-01, 9.2257e-08, 1.0115e-02]],
       grad_fn=<SoftmaxBackward0>)

$~ \\$

Calculating Attention-Weighted Context Vectors

The subsequent step is to use the Attention Weights earlier, to compute the weighted embedding vectors from V.

Input:

context_vectors = attention_weights @ V

print(context_vectors)

Output:

tensor([[-2.4015, -3.6157, -3.1565, -3.4481, -0.2659, -1.0132, -1.0527, -0.8838,
         -0.8617, -2.6299, -0.8879, -3.8774, -1.4376, -2.0597, -3.2499, -4.1146,
         -0.3537, -1.7522, -4.4342, -0.4208, -1.7473, -2.5230, -2.6547, -3.6916,
         -1.2874, -2.0094, -2.0400, -1.9443],
        [ 2.5695,  5.0923,  3.9690,  4.2990,  4.3684,  3.0220,  4.8688,  2.8423,
          4.6958,  3.9716,  5.8949,  3.6307,  2.4154,  3.7492,  4.7356,  6.9815,
          4.3885,  3.3385,  6.3139,  5.7449,  1.7411,  6.5813,  5.1148,  5.8224,
          3.6271,  3.8196,  4.8301,  5.6469],
        [-2.3355, -3.4879, -3.0844, -3.3353, -0.2875, -1.0540, -1.0939, -0.8983,
         -0.9252, -2.5819, -0.9411, -3.7367, -1.3410, -2.1087, -3.2195, -3.9842,
         -0.3826, -1.7398, -4.2849, -0.5222, -1.6938, -2.3847, -2.5709, -3.5644,
         -1.2504, -1.9646, -1.9809, -1.9704],
        [-2.4174, -3.6358, -3.1691, -3.4719, -0.2714, -1.0124, -1.0521, -0.8812,
         -0.8608, -2.6457, -0.8887, -3.9022, -1.4493, -2.0604, -3.2594, -4.1403,
         -0.3527, -1.7580, -4.4579, -0.4195, -1.7627, -2.5455, -2.6765, -3.7127,
         -1.2983, -2.0249, -2.0482, -1.9548],
        [ 2.5695,  5.0923,  3.9690,  4.2990,  4.3684,  3.0220,  4.8688,  2.8423,
          4.6958,  3.9716,  5.8949,  3.6307,  2.4154,  3.7492,  4.7356,  6.9815,
          4.3885,  3.3385,  6.3139,  5.7449,  1.7411,  6.5813,  5.1148,  5.8224,
          3.6271,  3.8196,  4.8301,  5.6469],
        [-1.2417, -1.0091, -1.7194, -1.3319, -0.9164, -2.1096, -2.0993, -1.2251,
         -2.5139, -1.9369, -2.3374, -1.0260,  0.7404, -3.4244, -2.8316, -1.5802,
         -1.1297, -1.7487, -1.5116, -3.0171, -0.7168,  0.3634, -1.1516, -1.0040,
         -0.5149, -1.2408, -0.8115, -2.9363]], grad_fn=<MmBackward0>)

$~ \\$

Summary: Packaging the self-attention mechanism in a PyTorch module

Let’s bring all the code together as a module, such that calling the forward pass would return the context vectors.

import math
import torch
import torch.nn.functional as F

class SelfAttention(nn.Module):
    
    def __init__(self, d, d_k, d_q, d_v):
        super(SelfAttention, self).__init__
        self.d = d
        self.d_k = d_k
        self.d_q = d_q
        self.d_v = d_v

        self.W_K = nn.Parameter(torch.rand(d,d_k))
        self.W_Q = nn.Parameter(torch.rand(d,d_q))
        self.W_V = nn.Parameter(torch.rand(d,d_v))
    
    def forward(self, X):
        K = X @ self.W_K
        Q = X @ self.W_Q
        V = X @ self.W_V

        attention_scores = Q @ K.T / math.sqrt(self.d_k)
        attention_weights = F.softmax(attention_scores, dim = -1)
        context_vector = attention_weights @ V

        return context_vector 

Okay! That’s the Scaled Dot-Product Self-Attention Mechanism implemented in code.

$~ \\$

2. References

This project post was primarily an exercise in re-implementing and modifying Sebastian Raschka’s excellent blog post on the same topic

I also found this code implementation by Mohd. Faraaz a good reference and sanity check.